palklion.blogg.se - Types of triangle isosceles

#TYPES OF TRIANGLE ISOSCELES FULL#
#TYPES OF TRIANGLE ISOSCELES CODE#
#TYPES OF TRIANGLE ISOSCELES SERIES#

When comparing floating-point numbers, you should always be careful to consider whether a strict equality is going to get you what you want.You could probably reasonably rule out lengths of 0 as well, to eliminate the possibility of degenerate triangles that just look like line segments or points. Checking to make sure the sides are non-negative is a great idea.Make sure you use the one the professor asks for. In C++, double and float are not the same thing.Looking at why this inequality has to hold: if the sum of two sides was exactly equal to the third side's length, you'd have a "degenerate" triangle where sides f and g could only lay on top of h! If they added up to less, the two sides could connect to the endpoints of h but then would never meet at a third point! You can test this yourself by cutting lengths of string or strips of paper and trying it out. However, it may be just as convenient for you to check all three cases. If you're dealing with isosceles or scalene triangles, you technically only need to check the smaller two sides against the largest side, and if it's true for them, it's true for the other two cases as well (why?). If you're dealing with equilateral triangles, you automatically know this condition is met (why?). :-)įor the sides to make a proper triangle, for each pair of sides (I'll call them f and g), they must add up to greater than the third side's length (I'll call it h). Don't be afraid to put on your math hat here and go wandering in, a little logic isn't a bad thing for a poli sci student to endure every now and then. But I'll give you some help with the "not a triangle" condition. It just involves a simple comparison of side lengths you don't have to go as far as angles. The logic falls out neatly from the definition of these different types of triangles, which as the professor notes, is information readily obtained from Wikipedia. Our professor has not covered this topic in class.

$types of triangle isosceles$

#TYPES OF TRIANGLE ISOSCELES CODE#

I currently have: //lab eleven program code on trianglesĮlse if(aside=bside || aside=cside || bside=cside)īut I need help with the if and else if statements to determine the type triangle. You may use the same values as in the example. Print the resulting triangle type to the console.Įnsure your Triangle detector works by running it 5 times as in the example above.

#TYPES OF TRIANGLE ISOSCELES SERIES#

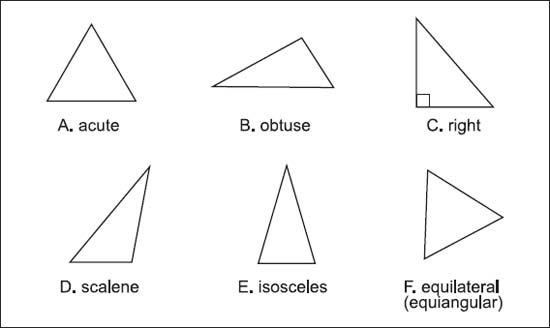
Use a series of nested if / else statements to determine if the triangle having side-lengths as set by the user is an EQUILATERAL, ISOSCELES, or SCALENE triangle. Repeat the last 2 steps twice more, once for each of the remaining 2 sides of the triangle. Set the user’s input to the variable you created representing the first side of the triangle. Prompt the user to input a value for the first side, then I need help with the following code that requires me to:ĭeclare 3 double type variables, each representing one of three sides of a triangle. This gives the order of rotational symmetry.Ī unique set of properties relating to the comparative length of its sides and the comparative size of its angles help to identify equilateral triangles, isosceles triangles, and scalene triangles.

#TYPES OF TRIANGLE ISOSCELES FULL#

Count how many ways the triangle will fit into its outline in a full turn (360°).

This gives the number of lines of symmetry of the triangle.

Count how many ways the triangle can be cut into a pair of mirrored halves.

Different numbers of arcs indicate different angles.

The same number of arcs indicate equal angles.

Different numbers of hash marks indicate different lengths.

The same number of hashes indicate equal lengths.

To classify a triangle using comparative lengths or angles:

Recognise that arcs in vertices can be used to indicate equal angles.

Recognise that hash marks indicate equal lengths.